Relativity and the Electromagnetic field

This week, I shall continue on the theme of the magnetic field and using a thought experiment prove the complete  interdependence of the electric and magnetic field, which we’ll see to be two ways of looking at the same thing. I first came across this fascinating line of reasoning in the pages of the second volume of the Feynman lectures on Physics, within which I have sought the most revealing wisdom on nature since my undergraduate days.

Consider a wire carrying current I and a charge at a distance l from it. The current will produce a magnetic field around the wire in the right-hand direction. The charge q is in the presence of the magnetic field, as shown in Fig: 1 below.

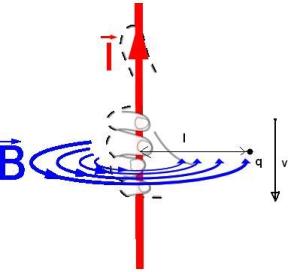
Fig: 1 Wire at rest, Charge moving down

Let us consider now that q is moving in a downward direction (note that current is in the upward direction) at a velocity equal to the drift velocity of electrons in the wire carrying current. Now, we shall analyse the forces on the system from two different inertial frames of reference and consider whether the observable results are the same, a requirement that is critical if we are to have any confidence in our methods of analyses. If our physical theory predicts different realities for observers in different inertial frames of reference, that would be a significant shortcoming indeed in the theory.

The first frame of reference is the one in which the wire is at rest. The current I is moving upwards and hence the drift electrons are moving downwards, say with a velocity v. The charge outside the wire, in its magnetic field is also moving down with the same velocity v. Since the wire is neutral, there is no electric force between it and the charge. But, since the charge moves in a magnetic field with a component of its velocity perpendicular to the field, there is a magnetic force on the charge. In this case, using the left hand rule, the force is towards the right if q is a positive charge and towards the left if q is negative. Assuming a positive q, observers in this frame of reference see the charge repelled from the wire. So, its velocity which was initially downwards, would now diverge away from the wire.

Let us now consider another frame of reference, this one moving at the same velocity as the charge and the drift electrons in the wire, as shown in Fig: 2 below.

Fig: 2 Wire moving up, Charge at rest

This would be like imagining the observer in a vessel moving downwards parallel to the motion of the external charge and the wire. In this frame of reference, the drift electrons are at rest and so there is no current in the wire. Hence, there is no magnetic field around the wire and no magnetic force on the charge. Does this mean the charge is at rest in this frame of reference? If so, in the previous frame, the charge should be seen as moving down at a constant velocity v. But, we had seen that the charge diverges away from the wire as it moves down. Since the observations in the two inertial frames have to agree with each other, there has to be something wrong with our reasoning in at least one frame.

In the second frame, since the charge is not moving, there is no magnetic force on it.  Maybe there is another force equivalent to the magnetic force in the first frame that will produce the same effect? One difference between the frames that we have ignored till now is that the wire is moving upward in the second frame and the electrons are at rest, while in the first frame, the wire is at rest and the electrons are moving down. When there is no current through the wire, the electrons and rest of the wire are at rest in the same frame and the charges balance each other. When there is a current and the electrons move downwards and wire is at rest, as in the first frame, according to special relativity, the charge of the electrons is unaffected by the velocity. But, the volume they occupy shrinks because the length of this space along the direction of the velocity shrinks according to the famous Lorentz transformation. Hence the charge density of electrons as seen in the first frame is higher than that in the second frame. By using a similar argument, we can see that the charge density of the positive charges in the wire is higher by the same amount, but in the second frame. So, we see that the second frame sees the wire as charged more positively than the first frame. In the first frame, we know that the wire is neutral. Otherwise, a wire will spontaneously attract or repel charges in its neighbourhood when the current through it is switched on. We see enough current carrying wires in common life to know this is not true. Hence, in the second frame, the wire is positively charged. As the charge q is also positive, it will be repelled from the wire. So, when we take the electric force also into consideration, the charge in the second frame repels from the wire, which when combined with the relative velocity of the second frame downwards with respect to the first, agrees with the observation in the first frame that the charge moved downwards in a divergent manner from the wire.

Similar observations in terms of velocity is arrived at  in both the frames of reference when we consider the effects of the electric and magnetic fields together. This adds to our understanding that they are but two facets of the general electromagnetic field. In different inertial frames, the electromagnetic field splits into different portions of electric and magneric fields and hence forces due to them. In our example, by choosing extremes of frames in which either the wire or the electrons were at rest, we could split the field into just the electric or just the magnetic field. But, many times it is a combination of both. By sacrificing a mathematical treatment of the problem, we have missed out on much elegance for the sake of simplicity. We also don’t know whether the velocities of the electron as seen in both the frames will agree in magnitude as well as in direction. They actually do, and they do this by having forces different in each frame in such a way as to have the velocities the same! I shall explore a mathematical treatment of the problem, again derived from Feynman’s lectures (Section 13-6), in a later post.